sábado, 19 de novembro de 2011
Geometria Espacial:Cilindro
Cilindro
* Introdução aos cilindros :
O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas.

Existem outras formas cilíndricas diferentes das comuns, como por exemplo o cilindro sinuzoidal obtido pela translação da função seno.
* Aplicações práticas: Os cilindros abaixo sugerem alguma aplicação importante em sua vida?



* A Construção de cilindros:
 Seja P um plano e nele vamos construir um círculo de raio r e tomemos também um segmento de reta AB que não seja paralelo ao plano P e nem esteja contido neste plano P. Um cilindro circular é a reunião de todos os segmentos congruentes e paralelos a AB com uma extremidade no círculo.
Seja P um plano e nele vamos construir um círculo de raio r e tomemos também um segmento de reta AB que não seja paralelo ao plano P e nem esteja contido neste plano P. Um cilindro circular é a reunião de todos os segmentos congruentes e paralelos a AB com uma extremidade no círculo.
Observamos que um cilindro é uma superfície no espaço R³, mas muitas vezes vale a pena considerar o cilindro como a região sólida contida dentro do cilindro. Quando nos referirmos ao cilindro como um sólido usaremos aspas, isto é, "cilindro" e quando for à superfície, simplesmente escreveremos cilindro.
A reta que contém o segmento AB é denominada geratriz e a curva que fica no plano do "chão" é a diretriz.
Em função da inclinação do segmento AB em relação ao plano do "chão", o cilindro será chamado reto ou oblíquo, respectivamente, se o segmento AB for perpendicular ou oblíquo ao plano que contém a curva diretriz.


* Objetos geométricos em um "cilindro":
Altura: A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".
Superfície Lateral: É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz.
Superfície Total: É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.
Área lateral: É a medida da superfície lateral do cilindro.
Área total: É a medida da superfície total do cilindro.
Seção meridiana de um cilindro: É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro.
* Extensão do conceito de cilindro:
As características apresentadas antes para cilindros circulares, são também possíveis para outros tipos de curvas diretrizes, como: elipse, parábola, hipérbole, seno ou outra curva simples e suave num plano.
Mesmo que a diretriz não seja uma curva conhecida, ainda assim existem cilindros obtidos quando a curva diretriz é formada por uma reunião de curvas simples. Por exemplo, se a diretriz é uma curva retangular, temos uma situação patológica e o cilindro recebe o nome especial de prisma.
Em função da curva diretriz, o cilindro terá o nome de cilindro: elíptico, parabólico, hiperbólico, sinuzoidal (telha de eternit).

* Classificação dos cilindros circulares:
Cilindro circular oblíquo: Apresenta as geratrizes oblíquas em relação aos planos das bases.
Cilindro circular reto: As geratrizes são perpendiculares aos planos das bases. Este tipo de cilindro é também chamado de cilindro de revolução, pois é gerado pela rotação de um retângulo.
Cilindro eqüilátero: É um cilindro de revolução cuja seção meridiana é um quadrado.
* Exercícios resolvidos :
1.Seja um cilindro circular reto de raio igual a 2cm e altura 3cm. Calcular a área lateral, área total e o seu volume.
A(base) = pi.r² = pi.2² = 4 pi cm²
A(lateral) = 2.pi.r.h = 2.pi.2.3 = 12 pi cm²
A(total) = A(lateral) + 2 A(base) = 12pi + 8pi = 20 pi cm²
Volume = A(base).h = pi.r²h = pi.4.3 = 12 pi cm³
* Introdução aos cilindros :
O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas.

Existem outras formas cilíndricas diferentes das comuns, como por exemplo o cilindro sinuzoidal obtido pela translação da função seno.
* Aplicações práticas: Os cilindros abaixo sugerem alguma aplicação importante em sua vida?



* A Construção de cilindros:
 Seja P um plano e nele vamos construir um círculo de raio r e tomemos também um segmento de reta AB que não seja paralelo ao plano P e nem esteja contido neste plano P. Um cilindro circular é a reunião de todos os segmentos congruentes e paralelos a AB com uma extremidade no círculo.
Seja P um plano e nele vamos construir um círculo de raio r e tomemos também um segmento de reta AB que não seja paralelo ao plano P e nem esteja contido neste plano P. Um cilindro circular é a reunião de todos os segmentos congruentes e paralelos a AB com uma extremidade no círculo.Observamos que um cilindro é uma superfície no espaço R³, mas muitas vezes vale a pena considerar o cilindro como a região sólida contida dentro do cilindro. Quando nos referirmos ao cilindro como um sólido usaremos aspas, isto é, "cilindro" e quando for à superfície, simplesmente escreveremos cilindro.
A reta que contém o segmento AB é denominada geratriz e a curva que fica no plano do "chão" é a diretriz.
Em função da inclinação do segmento AB em relação ao plano do "chão", o cilindro será chamado reto ou oblíquo, respectivamente, se o segmento AB for perpendicular ou oblíquo ao plano que contém a curva diretriz.


* Objetos geométricos em um "cilindro":
Em um cilindro, podemos identificar vários elementos:
Base: É a região plana contendo a curva diretriz e todo o seu interior. Num cilindro existem duas bases.
Eixo: É o segmento de reta que liga os centros das bases do "cilindro".Altura: A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".
Superfície Lateral: É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz.
Superfície Total: É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.
Área lateral: É a medida da superfície lateral do cilindro.
Área total: É a medida da superfície total do cilindro.
Seção meridiana de um cilindro: É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro.
* Extensão do conceito de cilindro:
As características apresentadas antes para cilindros circulares, são também possíveis para outros tipos de curvas diretrizes, como: elipse, parábola, hipérbole, seno ou outra curva simples e suave num plano.
Mesmo que a diretriz não seja uma curva conhecida, ainda assim existem cilindros obtidos quando a curva diretriz é formada por uma reunião de curvas simples. Por exemplo, se a diretriz é uma curva retangular, temos uma situação patológica e o cilindro recebe o nome especial de prisma.
Em função da curva diretriz, o cilindro terá o nome de cilindro: elíptico, parabólico, hiperbólico, sinuzoidal (telha de eternit).

* Classificação dos cilindros circulares:
Cilindro circular oblíquo: Apresenta as geratrizes oblíquas em relação aos planos das bases.
Cilindro circular reto: As geratrizes são perpendiculares aos planos das bases. Este tipo de cilindro é também chamado de cilindro de revolução, pois é gerado pela rotação de um retângulo.
Cilindro eqüilátero: É um cilindro de revolução cuja seção meridiana é um quadrado.
* Volume de um "cilindro" :
Em um cilindro, o volume é dado pelo produto da área da base pela altura.
V= A(base) h
Se a base é um círculo de raio r, e pi=3,141593..., então:
V = pi r² h
* Área lateral e área total de um cilindro circular reto :
Em um cilindro circular reto, a área lateral é dada por A(lateral)=2pi.r.h, onde r é o raio da base e h é a altura do cilindro. A área total corresponde à soma da área lateral com o dobro da área da base.
| A(total) = A(lateral) + 2 A(base) A(total) = 2 pi r h + 2 pi r² A(total) = 2 pi r(h+r) |  |
|---|
Exemplo: Um cilindro circular equilátero é aquele cuja altura é igual ao diâmetro da base, isto é h=2r. Neste caso, para calcular a área lateral, a área total e o volume, podemos usar as fórmulas, dadas por:
| A(lateral) = 4 pi r² A(base) = pi r² A(total) = A(lateral) + 2 A(base) = 6 pi r² Volume = A(base).h = pi r².2r = 2 pi r³ |  |
|---|
* Exercícios resolvidos :
1.Seja um cilindro circular reto de raio igual a 2cm e altura 3cm. Calcular a área lateral, área total e o seu volume.
A(base) = pi.r² = pi.2² = 4 pi cm²
A(lateral) = 2.pi.r.h = 2.pi.2.3 = 12 pi cm²
A(total) = A(lateral) + 2 A(base) = 12pi + 8pi = 20 pi cm²
Volume = A(base).h = pi.r²h = pi.4.3 = 12 pi cm³
2.Achar a área total da superfície de um cilindro reto, sabendo que o raio da base é de 10cm e a
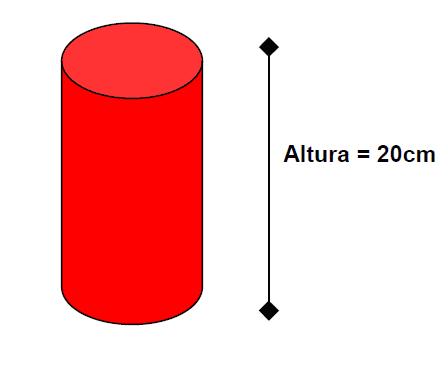 altura é de 20cm.
altura é de 20cm.
Solução:
A área de cada base é dada por Ab = πx r² ≈ 3,14 x 100 = 314cm² .
Quando planificamos a superfície lateral de um cilindro, obtemos
um retângulo no qual os lados têm a mesma altura h do cilindro e o
comprimento 2π da circunferência de uma das bases. Assim,
temos C = 2 x π x 10 ≈ 62,8cm. Desse modo, a área da superfície
lateral é Al ≈ 62,8 x 20 = 1.256cm².Assim, a área total da superfície
desse cilindro é At ≈ 314 + 314 + 1.256, o que resulta em
At ≈ 1.884cm²
3.A altura de um cilindro reto vale 6cm e o raio da base mede 2cm. Determine a área total e o volume do cilindro
Solução. Utilizando as fórmulas, temos:
i) .At= 2 π.R(R+h) = 2 π (2).(2+6)=2 π(2).(8)=32 πcm²
ii) .V= π R². h = π (2)² . (6)= 24 πcm³
 altura é de 20cm.
altura é de 20cm.Solução:
A área de cada base é dada por Ab = πx r² ≈ 3,14 x 100 = 314cm² .
Quando planificamos a superfície lateral de um cilindro, obtemos
um retângulo no qual os lados têm a mesma altura h do cilindro e o
comprimento 2π da circunferência de uma das bases. Assim,
temos C = 2 x π x 10 ≈ 62,8cm. Desse modo, a área da superfície
lateral é Al ≈ 62,8 x 20 = 1.256cm².Assim, a área total da superfície
desse cilindro é At ≈ 314 + 314 + 1.256, o que resulta em
At ≈ 1.884cm²
3.A altura de um cilindro reto vale 6cm e o raio da base mede 2cm. Determine a área total e o volume do cilindro
Solução. Utilizando as fórmulas, temos:
i) .At= 2 π.R(R+h) = 2 π (2).(2+6)=2 π(2).(8)=32 πcm²
ii) .V= π R². h = π (2)² . (6)= 24 πcm³
4. (FATEC) Sabe-se que um cilindro de revolução de raio igual a 10 cm, quando cortado por um plano paralelo ao eixo, a uma distância de 6 cm desse eixo, apresenta uma secção retangular equivalente à base. O volume desse cilindro, em centímetros cúbicos, é:
a) 1250π b)1250π² c)6,25π² d) 625π e)625π²
Solução. A figura mostra a secção (azul) a 6cm do eixo. Ela é um retângulo de dimensões (2x) e h. O valor de “x” pode ser calculado pela relação de Pitágoras:
10² = 6² + x² ---- > x = √100 - 36 = √64 = 8 cm
Logo (2x) = 16cm
Como a secção é equivalente à base, suas áreas são iguais:
{Abase =πR² = π (10)² =100 π
{Asecção = (2x) . h = 16. h
( 100 π ) 10000 π ²
V= π R² . h = π (10)² .-------- =-------------- = 625 π² cm ³
( 16 ) 16
5. (FGV) Em certa loja, as panelas são anunciadas de acordo com sua capacidade. Uma panela dessa loja, com a etiqueta "4 litros", tem 20cm de diâmetro. A altura dessa panela é aproximadamente:
a) 7cm b) 9cm c) 11cm d) 13cm e) 15cm.
Solução. O volume 4 litros corresponde em 4dm3 ou 4000cm3. O raio da panela mede 10cm. Aplicando a fórmula do volume do cilindro, temos:
(V cilindro = π R² . h 4000 40 ~
(V cilindro = 400 --- > ( 3,14 ) . (10) ² . h = 4000 -- > h = -------------- = ----- = 12,73 cm
( 3,14) . (100) 3,14
quinta-feira, 17 de novembro de 2011
Geometria Espacial:ESFERA
ESFERA
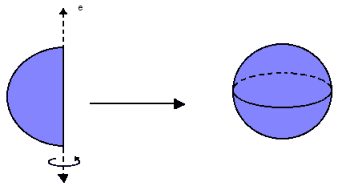
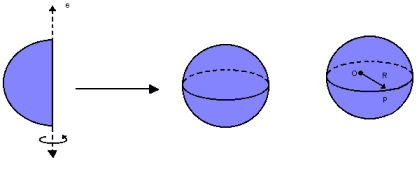
Chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R.Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior.
* Volume :
O volume da esfera de raio R é dado por:
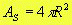
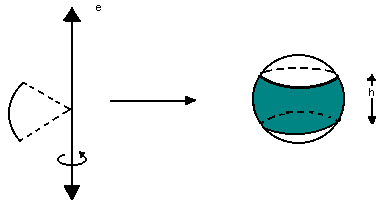
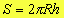
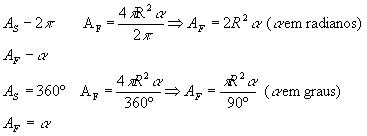
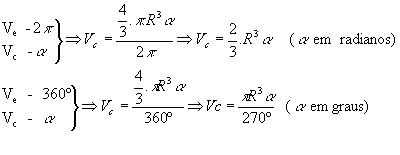
.jpg)
.jpg)

Chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R.Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior.

* Volume :
O volume da esfera de raio R é dado por:
* Partes da esfera:
Superfície esférica :
A superfície esférica de centro O e raio R é o conjunto de pontos do es[aço cuja distância ao ponto O é igual ao raio R.Se considerarmos a rotação completa de uma semicircunferência em torno de seu diâmetro, a superfície esférica é o resultado dessa rotação.

A área da superfície esférica é dada por:
* Zona esférica:
É a parte da esfera gerada do seguinte modo:
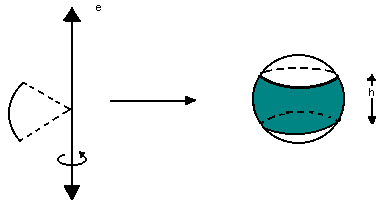
A área da zona esférica é dada por:
* Calota esférica :
É a parte da esfera gerada do seguinte modo:

Ä área da calota esférica é dada por:
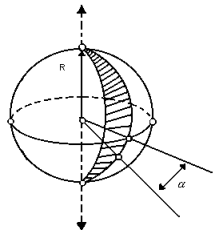
* Fuso esférico :
O fuso esférico é uma parte da superfície esférica que se obtém ao girar uma semi-circunferência de um ângulo 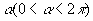 em torno de seu eixo:
em torno de seu eixo:

A área do fuso esférico pode ser obtida por uma regra de três simples:
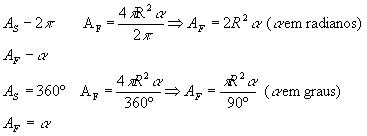
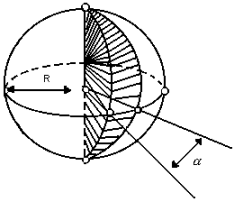
* Cunha esférica :
Parte da esfera que se obtém ao girar um semicírculo em torno de seu eixo de um ângulo 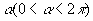 :
:

O volume da cunha pode ser obtido por uma regra de três simples:
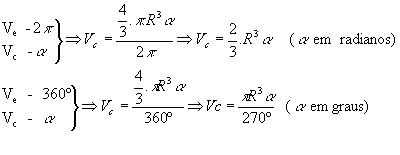
A esfera é obtida através da revolução da semicircunferência sobre um eixo. Podemos considerar que a esfera é um sólido.
Alguns conceitos básicos estão relacionados à esfera, se considerarmos a superfície esférica destacamos os seguintes elementos básicos:
Ø Pólos
Ø Equador
Ø Paralelo
Ø Meridiano
Área de uma superfície esférica
Temos que a área de uma superfície esférica de raio r é igual a:
Volume da esfera
Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:
Posição relativa entre plano e esfera
Plano secante à esfera :
O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.
Plano tangente à esfera :
O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.
Plano externo à esfera :
O plano e a esfera não possuem pontos em comum.
.jpg)
esfera possui inúmeras aplicações, como exemplo podemos citar a Óptica (Física), a seção de uma esfera forma uma lente esférica, que são objetos importantes na construção de óculos. Corpos esféricos possuem grande importância na Engenharia Mecânica, a parte interior de inúmeras peças capazes de realizar movimentos circulares sobre eixos é constituída de esferas de aço. Um bom exemplo dessas peças é o rolamento.
* Exercícios resolvidos :
1. (FFT) Considere a Terra como uma esfera de raio 6.370km. Qual é sua área superficial? Descobrir a área da superfície coberta de água, sabendo que ela corresponde a aproximadamente 3/4 da superfície total.

Solução:
At = 4PI x r2 = 4 x 3,14 x 40.576.900. Portanto, At = 509.650.000km2. A superfície coberta por águas é dada por Aa = 3/4 x 509.650.000. Logo, Aa = 382.224km2.
2. – UFPB/93 – Sendo o volume de uma esfera de raio R numericamente igual a 33 vezes a sua área, calcular o valor de R, em unidades de comprimento.
Solução:
Sabemos que para uma esfera de raio R, são válidas as seguintes fórmulas para o cálculo do volume V e da área S:
V = (4/3).p .R3 e S = 4.p .R2
O problema exige que V = 33.S ; substituindo, vem:
(4/3).p .R3 = 33.4.p .R2 Þ (4/3).R3 = 132.R2 Þ (4/3).R = 132 Þ R = 132/(4/3) = 132.(3/4) = 396/4 = 99
Resposta: 99 u.c.
3.Uma fábrica de bombons deseja produzir 20 000 unidades no formato de uma esfera de raio 1 cm. Determine o volume de cada bombom e a quantidade de chocolate necessária para produzir esse número de bombons.
A quantidade de chocolate necessária para a produção das 20 000 unidades é de:
4,18 * 20 000 = 83 600 cm³
Sabemos que 1cm³ = 1 ml, então 83 600 cm³ corresponde a 83 600 ml de chocolate ou 83,6 quilos.
A fábrica irá gastar 83,6 quilos de chocolate, e o volume de cada bombom será de 4,18 cm³.
Geometria Espacial:Cones
Cones
 Denominamos cone ao sólido formado pela reunião de todos os segmentos de reta que têm uma extremidade em um ponto P (vértice) e a outra num ponto qualquer da região.
Denominamos cone ao sólido formado pela reunião de todos os segmentos de reta que têm uma extremidade em um ponto P (vértice) e a outra num ponto qualquer da região.
*Elementos do cone :
Em um cone, podem ser identificados vários elementos:

1.Vértice de um cone é o ponto P, onde concorrem todos os segmentos de reta.
2.Base de um cone é a região plana contida no interior da curva, inclusive a própria curva.
3.Eixo do cone é quando a base do cone é uma região que possui centro, o eixo é o segmento de reta que passa pelo vértice P e pelo centro da base.
4.Geratriz é qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.
5.Altura é a distância do vértice do cone ao plano da base.
6.Superfície lateral de um cone é a reunião de todos os segmentos de reta que tem uma extremidade em P e a outra na curva que envolve a base.
7.Superfície do cone é a reunião da superfície lateral com a base do cone que é o círculo.
8.Seção meridiana de um cone é uma região triangular obtida pela interseção do cone com um plano que contem o eixo do mesmo.
* Classificação do cone :
Ao observar a posição relativa do eixo em relação à base, os cones podem ser classificados como retos ou oblíquos. Um cone é dito reto quando o eixo é perpendicular ao plano da base e é oblíquo quando não é um cone reto. Ao lado apresentamos um cone oblíquo.
 Observação: Para efeito de aplicações, os cones mais importantes são os cones retos. Em função das bases, os cones recebem nomes especiais. Por exemplo, um cone é dito circular se a base é um círculo e é dito elíptico se a base é uma região elíptica.
Observação: Para efeito de aplicações, os cones mais importantes são os cones retos. Em função das bases, os cones recebem nomes especiais. Por exemplo, um cone é dito circular se a base é um círculo e é dito elíptico se a base é uma região elíptica.
*Observações sobre um cone circular reto:
Um cone circular reto é denominado cone de revolução por ser obtido pela rotação (revolução) de um triângulo retângulo em torno de um de seus catetos

A seção meridiana do cone circular reto é a interseção do cone com um plano que contem o eixo do cone. Na figura ao lado, a seção meridiana é a região triangular limitada pelo triângulo isósceles VAB.Em um cone circular reto, todas as geratrizes são congruentes entre si. Se g é a medida da geratriz então, pelo Teorema de Pitágoras, temos uma relação notável no cone: g²=h²+r², que pode ser "vista" na figura abaixo:

A Área Lateral de um cone circular reto pode ser obtida em função de g (medida da geratriz) e r (raio da base do cone):
A(lateral) = pi.r.g
A Área total de um cone circular reto pode ser obtida em função de g (medida da geratriz) e r (raio da base do cone):
A(total) = pi.r.g + pi.r² = = pi.r.(g+r)
* Cones Equiláteros :
Um cone circular reto é um cone equilátero se a sua seção meridiana é uma região triangular equilátera e neste caso a medida da geratriz é igual à medida do diâmetro da base.

A área da base do cone é dada por:
A(base) = pi r²
Pelo Teorema de Pitágoras temos que (2r)²=h²+r², logo h²=4r²-r²=3r², assim:
h = r
Como o volume do cone é obtido por 1/3 do produto da área da base pela altura, então:
V=(1/3) pi √3 r³
Como a área lateral pode ser obtida por:
A(lateral) = pi.r.g = pi.r.2r = 2.pi.r²
então a área total será dada por:
A(total) = 3 pi r²
* Exercícios resolvidos :
Notação: Usaremos a notação R[3] para representar a raiz quadrada de 3.
1.A geratriz de um cone circular reto mede 20 cm e forma um ângulo de 60 graus com o plano da base. Determinar a área lateral, área total e o volume do cone.
Como sen(60o)=h/20, então:
(1/2) R[3] = h/20
h = 10 R[3] cm
Como V = (1/3)×(A(base).h, então:
V = (1/3) pi.r²h
V = (1/3) pi.10².10 R[3]
V = (1/3) 1000.R[3].pi cm³


Se r=10cm; g=20cm e A(lateral)=pi.r.g, escreveremos:
A(lataral) = pi.r.g = pi.10.20 = 200.pi cm²
A(total) = A(lateral) + A(base)
= pi.r.g + pi.r² = pi.r.(r+g)
= pi.10.(10+20) = 300 pi cm²
2. A hipotenusa de um triângulo retângulo mede 2cm e um dos ângulos mede 60 graus. Girando-se o triângulo em torno do cateto menor, obtem-se um cone. Qual é o seu volume? Como sen(60º)=r/2, segue que:
R[3]/2 = r/2
 r = R[3] cm
r = R[3] cm
Substituindo os valores de g e de r, na relação g²=h²+r², obtemos
h = 1cm
V = (1/3).A(base).h = (1/3) pi.r²h
= (1/3).pi.3 = pi cm³
3.Os catetos de um triângulo retângulo medem b e c, e a sua área mede 2m². O cone obtido pela rotação do triângulo em torno do cateto b tem volume 16 pi m³. Obteremos a medida do cateto c. Como a área do triângulo mede 2m², segue que: (1/2)bc=2, o que garante que bc=4. Como a área da base é dada por A(base)=pi.r²=pi.c², temos que
V = 16 pi = (1/3) pi c² b
c = 12 m
4.As áreas das bases de um cone circular reto e de um prisma quadrangular reto são iguais. O prisma tem altura 12 cm e volume igual ao dobro do volume do cone. Determinar a altura do cone.
Se
h(prisma) = 12
A(base do prisma) = A(base do cone) = A
V(prisma) = 2×V(cone)
assim:
A×h(prisma) = 2(A h)/3
A 12 = (2/3)A h
h = 18 cm
5.Anderson colocou uma casquinha de sorvete dentro de uma lata cilíndrica de mesma base, mesmo raio r e mesma altura h da casquinha. Qual é o volume do espaço (vazio) compreendido entre a lata e a casquinha de sorvete?
V = V(cilindro) - V(cone)
= A(base).h - (1/3) A(base).h
= pi.r².h - (1/3).pi.r².h
= (2/3) pi.r².h cm³
*O conceito de cone :
Considere uma região plana limitada por uma curva suave (sem quinas), fechada e um ponto P fora desse plano.
*Elementos do cone :
Em um cone, podem ser identificados vários elementos:

1.Vértice de um cone é o ponto P, onde concorrem todos os segmentos de reta.
2.Base de um cone é a região plana contida no interior da curva, inclusive a própria curva.
3.Eixo do cone é quando a base do cone é uma região que possui centro, o eixo é o segmento de reta que passa pelo vértice P e pelo centro da base.
4.Geratriz é qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.
5.Altura é a distância do vértice do cone ao plano da base.
6.Superfície lateral de um cone é a reunião de todos os segmentos de reta que tem uma extremidade em P e a outra na curva que envolve a base.
7.Superfície do cone é a reunião da superfície lateral com a base do cone que é o círculo.
8.Seção meridiana de um cone é uma região triangular obtida pela interseção do cone com um plano que contem o eixo do mesmo.
* Classificação do cone :
Ao observar a posição relativa do eixo em relação à base, os cones podem ser classificados como retos ou oblíquos. Um cone é dito reto quando o eixo é perpendicular ao plano da base e é oblíquo quando não é um cone reto. Ao lado apresentamos um cone oblíquo.

*Observações sobre um cone circular reto:
Um cone circular reto é denominado cone de revolução por ser obtido pela rotação (revolução) de um triângulo retângulo em torno de um de seus catetos

A seção meridiana do cone circular reto é a interseção do cone com um plano que contem o eixo do cone. Na figura ao lado, a seção meridiana é a região triangular limitada pelo triângulo isósceles VAB.Em um cone circular reto, todas as geratrizes são congruentes entre si. Se g é a medida da geratriz então, pelo Teorema de Pitágoras, temos uma relação notável no cone: g²=h²+r², que pode ser "vista" na figura abaixo:

A Área Lateral de um cone circular reto pode ser obtida em função de g (medida da geratriz) e r (raio da base do cone):
A(lateral) = pi.r.g
A Área total de um cone circular reto pode ser obtida em função de g (medida da geratriz) e r (raio da base do cone):
A(total) = pi.r.g + pi.r² = = pi.r.(g+r)
* Cones Equiláteros :
Um cone circular reto é um cone equilátero se a sua seção meridiana é uma região triangular equilátera e neste caso a medida da geratriz é igual à medida do diâmetro da base.

A área da base do cone é dada por:
A(base) = pi r²
Pelo Teorema de Pitágoras temos que (2r)²=h²+r², logo h²=4r²-r²=3r², assim:
h = r

Como o volume do cone é obtido por 1/3 do produto da área da base pela altura, então:
V=(1/3) pi √3 r³
Como a área lateral pode ser obtida por:
A(lateral) = pi.r.g = pi.r.2r = 2.pi.r²
então a área total será dada por:
A(total) = 3 pi r²
* Exercícios resolvidos :
Notação: Usaremos a notação R[3] para representar a raiz quadrada de 3.
1.A geratriz de um cone circular reto mede 20 cm e forma um ângulo de 60 graus com o plano da base. Determinar a área lateral, área total e o volume do cone.
Como sen(60o)=h/20, então:
(1/2) R[3] = h/20
h = 10 R[3] cm
Como V = (1/3)×(A(base).h, então:
V = (1/3) pi.r²h
V = (1/3) pi.10².10 R[3]
V = (1/3) 1000.R[3].pi cm³


Se r=10cm; g=20cm e A(lateral)=pi.r.g, escreveremos:
A(lataral) = pi.r.g = pi.10.20 = 200.pi cm²
A(total) = A(lateral) + A(base)
= pi.r.g + pi.r² = pi.r.(r+g)
= pi.10.(10+20) = 300 pi cm²
2. A hipotenusa de um triângulo retângulo mede 2cm e um dos ângulos mede 60 graus. Girando-se o triângulo em torno do cateto menor, obtem-se um cone. Qual é o seu volume? Como sen(60º)=r/2, segue que:
R[3]/2 = r/2
 r = R[3] cm
r = R[3] cmSubstituindo os valores de g e de r, na relação g²=h²+r², obtemos
h = 1cm
V = (1/3).A(base).h = (1/3) pi.r²h
= (1/3).pi.3 = pi cm³
3.Os catetos de um triângulo retângulo medem b e c, e a sua área mede 2m². O cone obtido pela rotação do triângulo em torno do cateto b tem volume 16 pi m³. Obteremos a medida do cateto c. Como a área do triângulo mede 2m², segue que: (1/2)bc=2, o que garante que bc=4. Como a área da base é dada por A(base)=pi.r²=pi.c², temos que
V = 16 pi = (1/3) pi c² b
c = 12 m
4.As áreas das bases de um cone circular reto e de um prisma quadrangular reto são iguais. O prisma tem altura 12 cm e volume igual ao dobro do volume do cone. Determinar a altura do cone.
Se
h(prisma) = 12
A(base do prisma) = A(base do cone) = A
V(prisma) = 2×V(cone)
assim:
A×h(prisma) = 2(A h)/3
A 12 = (2/3)A h
h = 18 cm
5.Anderson colocou uma casquinha de sorvete dentro de uma lata cilíndrica de mesma base, mesmo raio r e mesma altura h da casquinha. Qual é o volume do espaço (vazio) compreendido entre a lata e a casquinha de sorvete?
V = V(cilindro) - V(cone)
= A(base).h - (1/3) A(base).h
= pi.r².h - (1/3).pi.r².h
= (2/3) pi.r².h cm³
Geometria Espacial:Pirâmide
Pirâmide
Utilizaremos R[z] para denotar a raiz quadrada de z>0.
*O conceito de pirâmide:
Consideremos um polígono contido em um plano (por exemplo, o plano horizontal) e um ponto V localizado fora desse plano. Uma Pirâmide é a reunião de todos os segmentos que têm uma extremidade em P e a outra num ponto qualquer do polígono. O ponto V recebe o nome de vértice da pirâmide.
 Exemplo: As pirâmides do Egito, eram utilizadas para sepultar faraós, bem como as pirâmides no México e nos Andes, que serviam a finalidades de adoração aos seus deuses. As formas piramidais eram usadas por tribos indígenas e mais recentemente por escoteiros para construir barracas.
Exemplo: As pirâmides do Egito, eram utilizadas para sepultar faraós, bem como as pirâmides no México e nos Andes, que serviam a finalidades de adoração aos seus deuses. As formas piramidais eram usadas por tribos indígenas e mais recentemente por escoteiros para construir barracas.* Elementos de uma pirâmide:
Em uma pirâmide, podemos identificar vários elementos:
 Base: A base da pirâmide é a região plana poligonal sobre a qual se apoia a pirâmide.
Base: A base da pirâmide é a região plana poligonal sobre a qual se apoia a pirâmide.Vértice: O vértice da pirâmide é o ponto isolado P mais distante da base da pirâmide.
Eixo: Quando a base possui um ponto central, isto é, quando a região poligonal é simétrica ou regular, o eixo da pirâmide é a reta que passa pelo vértice e pelo centro da base.
Altura: Distância do vértice da pirâmide ao plano da base.
Faces laterais: São regiões planas triangulares que passam pelo vértice da pirâmide e por dois vértices consecutivos da base.
Arestas Laterais: São segmentos que têm um extremo no vértice da pirâmide e outro extremo num vértice do polígono situado no plano da base.
Apótema: É a altura de cada face lateral.
Superfície Lateral: É a superfície poliédrica formada por todas as faces laterais.
Aresta da base: É qualquer um dos lados do polígono da base.
* Classificação das pirâmides pelo número de lados da base:
| triangular | quadrangular | pentagonal | hexagonal |
|---|---|---|---|
 |  |  |  |
| base:triângulo | base:quadrado | base:pentágono | base:hexágono |
* Pirâmide Regular reta :
Pirâmide regular reta é aquela que tem uma base poligonal regular e a projeção ortogonal do vértice V sobre o plano da base coincide com o centro da base.
 | R | raio do circulo circunscrito |
|---|---|---|
| r | raio do círculo inscrito | |
| l | aresta da base | |
| ap | apótema de uma face lateral | |
| h | altura da pirâmide | |
| al | aresta lateral | |
| As faces laterais são triângulos isósceles congruentes | ||
* Área Lateral de uma pirâmide:
Às vezes podemos construir fórmulas para obter as áreas das superfícies que envolvem um determinado sólido. Tal processo é conhecido como a planificação desse sólido. Isto pode ser realizado se tomarmos o sólido de forma que a sua superfície externa seja feita de papelão ou algum outro material.
No caso da pirâmide, a idéia é tomar uma tesoura e cortar (o papelão d)a pirâmide exatamente sobre as arestas, depois reunimos as regiões obtidas num plano que pode ser o plano de uma mesa.

As regiões planas obtidas são congruentes às faces laterais e também à base da pirâmide.
Se considerarmos uma pirâmide regular cuja base tem n lados e indicarmos por A(face) a área de uma face lateral da pirâmide, então a soma das áreas das faces laterais recebe o nome de área lateral da pirâmide e pode ser obtida por:
A(lateral) = n A(face)
Exemplo: Seja a pirâmide quadrangular regular que está planificada na figura acima, cuja aresta da base mede 6cm e cujo apótema mede 4cm.
Como A(lateral)=n.A(face) e como a pirâmide é quadrangular temos n=4 triângulos isósceles, a área da face lateral é igual à área de um dos triângulos, assim:
| A(face) = b h/2 = 6.4/2 = 12 A(lateral) = 4.12 = 48 cm² |  |
|---|
Exemplo: A aresta da base de uma pirâmide hexagonal regular mede 8 cm e a altura 10 cm. Calcular a área lateral.Tomaremos a aresta com a=8 cm e a altura com h=10 cm. Primeiro vamos calcular a medida do apótema da face lateral da pirâmide hexagonal. Calcularemos o raio r da base.Como a base é um hexágono regular temos que r=(a/2)R[3], assim r=8R[3]/2=4R[3] e pela relação de Pitágoras, segue que (ap)²=r²+h², logo:

(ap)²= (4R[3])²+10² = 48+100 = 148 = 4·37 = 2R[37]
*Área total de uma Pirâmide:
A área total de uma pirâmide é a soma da área da base com a área lateral, isto é:
A(total) = A(lateral) + A(base)
Exemplo: As faces laterais de uma pirâmide quadrangular regular formam ângulos de 60 graus com a base e têm as arestas da base medindo 18 cm. Qual é a área total?
Já vimos que A(lateral)=n.A(face) e como cos(60º)=(lado/2)/a, então 1/2=9/a donde segue que a=18, assim:
A(face) = b.h/2 = (18.18)/2 = 162
A(lateral) = 4.162 = 648
A(base) = 18² = 324
Concluímos que:
A(total) = A(lateral) + A(base) = 648+324 = 970
Exemplo: Um grupo de escoteiros quer obter a área total de suas barracas, as quais têm forma piramidal quadrangular. Para isso, eles usam medidas escoteiras. Cada dois passos de um escoteiro mede 1 metro. A barraca tem 4 passos escoteiros de lado da base e 2 passos de apótema. Calcular a área da base, área lateral e a área total.

A(base) = 2.2 = 4 m²
A(lateral) = 4.2.1 = 8 m³
Logo, a área total da barraca é:
A(total) = A(lateral) + A(base) = 8+4 = 12 m²
* Volume de uma Pirâmide:
O volume de uma pirâmide pode ser obtido como um terço do produto da área da base pela altura da pirâmide, isto é:
Volume = (1/3) A(base) h

Exemplo: Juliana tem um perfume contido em um frasco com a forma de uma pirâmide regular com base quadrada. A curiosa Juliana quer saber o volume de perfume que o frasco contém. Para isso ela usou uma régua e tirou duas informações: a medida da aresta da base de 4cm e a medida da aresta lateral de 6cm.
Como V(pirâmide)=A(base).h/3, devemos calcular a área da base e a medida da altura. Como a base tem forma quadrada de lado a=4cm, temos que A(base)=a²=4cm.4cm=16 cm².
 A altura h da pirâmide pode ser obtida como a medida de um cateto de um triângulo retângulo cuja hipotenusa é dada pela altura L=6cm da aresta lateral e o outro cateto Q=2×R[2] que é a metade da medida da diagonal do quadrado. Dessa forma h²=L²-Q², se onde segue que h²=36-8=28 e assim temos que h=2R[7] e o volume será dado por V=(1/3).16.2R[7]=(32/3)R[7].
A altura h da pirâmide pode ser obtida como a medida de um cateto de um triângulo retângulo cuja hipotenusa é dada pela altura L=6cm da aresta lateral e o outro cateto Q=2×R[2] que é a metade da medida da diagonal do quadrado. Dessa forma h²=L²-Q², se onde segue que h²=36-8=28 e assim temos que h=2R[7] e o volume será dado por V=(1/3).16.2R[7]=(32/3)R[7].* Seção Transversal de uma pirâmide:
Seção transversal de uma pirâmide é a interseção da pirâmide com um plano paralelo à base da mesma. A seção transversal tem a mesma forma que a base, isto é, as suas arestas correspondentes são proporcionais. A razão entre uma aresta da seção transversal e uma aresta correspondente da base é dita razão de semelhança.
Observações sobre seções transversais:
Em uma pirâmide qualquer, a seção transversal e a base são regiões poligonais semelhantes. A razão entre a área da seção transversal e a área da base é igual ao quadrado da razão de semelhança.
Ao seccionar uma pirâmide por um plano paralelo à base, obtemos outra pirâmide menor (acima do plano) semelhante em todos os aspectos à pirâmide original.
Se duas pirâmides têm a mesma altura e as áreas das bases são iguais, então as seções transversais localizadas à mesma distância do vértice têm áreas iguais.
 | V(seção) | Volume da seção até o vértice (volume da pirâmide menor) |
|---|---|---|
| V(piram) | Volume da pirâmide (maior) | |
| A(seção) | Área da seção transversal (base da pirâmide menor) | |
| A(base) | Área da base da pirâmide (maior) | |
| h | Distância do vértice à seção (altura da pirâmide menor) | |
| H | Altura da pirâmide (maior) |
Assim:
| V(seção) V(base) | = | A(seção) A(piram) | · | h H |
|---|
| A(seção) A(base) | = | h² H² |
|---|
|
Exemplo: Uma pirâmide tem a altura medindo 9cm e volume igual a 108cm³. Qual é o volume do tronco desta pirâmide, obtido pelo corte desta pirâmide por um plano paralelo à base da mesma, sabendo-se que a altura do tronco da pirâmide é 3cm?
Como:
V(pirMenor)/V(pirâmide) = h³/H³
V(pirMenor)/108 = 6³/9³
V(pirMenor) = 32
então:
V(tronco)=V(pirâmide)-V(pirMenor)= 108cm³-2cm³ = 76 cm³
Exercícios resolvidos :
altura aproximada de 147m. Qual é o seu volume?
Solução:
A base da pirâmide é um quadrado com lados de 230m.
Logo, a área da base é dada por: Ab = 230 x 230 = 52.900m
2.Como o volume é dado por V = 1/3 x Ab x h, temos: V = 1/3 x
52.900 x 147. Portanto, V = 2.592.100m
2.Um tronco da pirâmide possui como bases dois quadrados de lados medindo 16 e 24 centímetros, respectivamente. Sabendo que a altura do tronco é equivalente a 42 cm, determine seu volume.
Área quadrado maior: 24 * 24 = 576 cm²
Área quadrado menor: 16 * 16 = 256 cm²
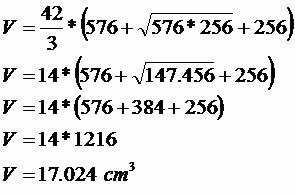
3.Um reservatório possui as dimensões de um tronco da pirâmide com lado da base menor medindo 2 m e lado da base maior medindo 8 m. Considerando que a medida da altura corresponde a √8 m, calcule sua capacidade de armazenamento.
Área quadrado maior: 8 * 8 = 64 m²
Área quadrado menor: 2 * 2 = 4 m²
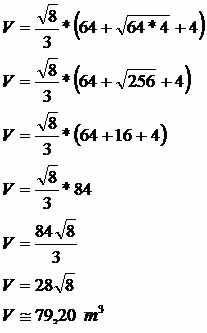
Assinar:
Postagens (Atom)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)

